974. Floyd – 1

A complete directed weighted graph is given by its adjacency matrix. Construct a matrix of the shortest paths between all pairs of its vertices. It is guaranteed that the graph has no cycles of negative weight.

Input. The first line contains the number of vertices n (1 ≤ n ≤ 100) in the graph. Each of the next n lines contains n integers and describes the adjacency matrix of the graph (the j-th number in the i-th row corresponds to the weight of the edge from vertex i to vertex j). All numbers by the absolute value do not exceed 100. The diagonal elements of the matrix are always zeros.

Output. Print n lines with n integers – the matrix of the shortest distances between all pairs of vertices. The j-th number in the i-th row should equal the weight of the shortest path from vertex i to vertex j.

Sample input	Sample output
4 0 5 9 100 100 0 2 8 100 100 0 7 4 100 100 0	0 5 7 13 12 0 2 8 11 16 0 7 4 9 11 0

SOLUTION

graphs – Floyd – Warshall

Algorithm analysis

In this problem you must construct a matrix of the shortest paths between all pairs of vertices in a graph. To do this, the Floyd-Warshall algorithm should be implemented.

Example

The graph described in the problem statement is as follows:

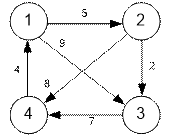
Algorithm realization

Store the adjacency matrix of the graph in the array g.

#define MAX 101

int g[MAX][MAX];

The floyd function implements the Floyd – Warshall algorithm.

void floyd(void)

{

int i, j, k;

for(k = 0; k < n; k++)

for(i = 0; i < n; i++)

for(j = 0; j < n; j++)

if (g[i][k] + g[k][j] < g[i][j]) g[i][j] = g[i][k] + g[k][j];

}

The main part of the program. Read the input graph.

scanf("%d",&n);

for(i = 0; i < n; i++)

for(j = 0; j < n; j++)

scanf("%d",&g[i][j]);

Run the Floyd – Warshall algorithm.

floyd();

Print the matrix of the shortest distances between all pairs of vertices.

for(i = 0; i < n; i++)

{

for(j = 0; j < n; j++)

printf("%d ",g[i][j]);

printf("\n");

}

Java realization

import java.util.*;

public class Main

{

static int g[][];

static int n;

static void floyd()

{

for(int k = 0; k < n; k++)

for(int i = 0; i < n; i++)

for(int j = 0; j < n; j++)

if (g[i][k] + g[k][j] < g[i][j])

g[i][j] = g[i][k] + g[k][j];

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

n = con.nextInt();

g = new int[n][n];

for(int i = 0; i < n; i++)

for(int j = 0; j < n; j++)

g[i][j] = con.nextInt();

floyd();

for (int i = 0; i < n; i++)

{

for (int j = 0; j < n; j++)

System.out.print(g[i][j] + " ");

System.out.println();

}

con.close();

}

}

Python realization

The floyd function implements the Floyd – Warshall algorithm.

def floyd():

for k in range(n):

for i in range(n):

for j in range(n):

if g[i][k] + g[k][j] < g[i][j]:

g[i][j] = g[i][k] + g[k][j]

The main part of the program. Read the input graph.

n = int(input())

g = [[] for _ in range(n)]

for i in range(n):

g[i] = list(map(int, input().split()))

Run the Floyd – Warshall algorithm.

floyd()

Print the matrix of the shortest distances between all pairs of vertices.

for i in range(n):

print(*g[i])